Abstract
Provenance is information about entities, activities, and people involved in producing a piece of data or thing, which can be used to form assessments about its quality, reliability or trustworthiness. PROV-DM is the conceptual data model that forms a basis for the W3C provenance (PROV) family of specifications. PROV-DM distinguishes core structures, forming the essence of provenance information, from extended structures catering for more specific uses of provenance. PROV-DM is organized in six components, respectively dealing with: (1) entities and activities, and the time at which they were created, used, or ended; (2) derivations of entities from entities; (3) agents bearing responsibility for entities that were generated and activities that happened; (4) a notion of bundle, a mechanism to support provenance of provenance; (5) properties to link entities that refer to the same thing; and, (6) collections forming a logical structure for its members.
This document introduces inferences and definitions
that are allowed on provenance statements and constraints
that PROV instances must satisfy in order to be considered
valid. These inferences and constraints are useful for
readers who develop applications that generate provenance or reason
over provenance. They can also be used to normalize PROV
instances to forms that can easily be compared in order to determine
whether two PROV instances are equivalent.
Status of This Document
This section describes the status of this document at the time of its publication. Other documents may supersede this document. A list of current W3C publications and the latest revision of this technical report can be found in the W3C technical reports index at http://www.w3.org/TR/.
Last Call
This is the second public release of the PROV-CONSTRAINTS document.
This is a Last Call Working Draft. The design is not expected to change significantly, going forward, and now is the key time for external review.
This specification identifies features at
risk related to the at-risk Mention feature of [PROV-DM]:
Inference 24 (mention-specialization) and
Constraint 33 (mention-unique).
These might be removed from PROV-CONSTRAINTS.
PROV Family of Specifications
This document is part of the PROV family of specifications, a set of specifications defining various aspects that are necessary to achieve the vision of inter-operable
interchange of provenance information in heterogeneous environments such as the Web. The specifications are:
- PROV-DM, the PROV data model for provenance;
- PROV-CONSTRAINTS, a set of constraints applying to the PROV data model (this document);
- PROV-N, a notation for provenance aimed at human consumption;
- PROV-O, the PROV ontology, an OWL2 ontology allowing the mapping of PROV to RDF;
- PROV-AQ, the mechanisms for accessing and querying provenance;
- PROV-PRIMER, a primer for the PROV data model.
How to read the PROV Family of Specifications
- The primer is the entry point to PROV offering an introduction to the provenance model.
- The Linked Data and Semantic Web community should focus on PROV-O defining PROV classes and properties specified in an OWL2 ontology. For further details, PROV-DM and PROV-CONSTRAINTS specify the constraints applicable to the data model, and its interpretation. PROV-SEM provides a mathematical semantics.
- Developers seeking to retrieve or publish provenance should focus on PROV-AQ.
- Readers seeking to implement other PROV serializations
should focus on PROV-DM and PROV-CONSTRAINTS. PROV-O and PROV-N offer examples of mapping to RDF and text, respectively.
This document was published by the Provenance Working Group as an Editor's Draft. If you wish to make comments regarding this document, please send them to public-prov-comments@w3.org (subscribe, archives). All feedback is welcome.
Publication as an Editor's Draft does not imply endorsement by the W3C Membership. This is a draft document and may be updated, replaced or obsoleted by other documents at any time. It is inappropriate to cite this document as other than work in progress.
This document was produced by a group operating under the 5 February 2004 W3C Patent Policy. W3C maintains a public list of any patent disclosures made in connection with the deliverables of the group; that page also includes instructions for disclosing a patent. An individual who has actual knowledge of a patent which the individual believes contains Essential Claim(s) must disclose the information in accordance with section 6 of the W3C Patent Policy.
1. Introduction
Provenance is a record that describes the people, institutions,
entities, and activities, involved in producing, influencing, or
delivering a piece of data or a thing. This document complements
the PROV-DM specification [PROV-DM] that defines a data model for
provenance on the Web.
1.1 Conventions
The key words "must", "must not", "required", "shall", "shall
not", "should", "should not", "recommended", "may", and
"optional" in this document are to be interpreted as described in
[RFC2119].
In this document, logical formulas contain variables written as
lower-case identifiers. Some of these ariables are written
beginning with the underscore character _, by convention, to indicate that they
(intentionally) appear only once in the formula; thus, the textual
variable name is mnemonic only.
1.2 Purpose of this document
The PROV Data Model, PROV-DM, is a conceptual data model for provenance, which is
realizable using different serializations such as PROV-N and PROV-O.
A PROV instance is a set of PROV statements,
possibly including bundles, or named sets of statements. For
example, such a PROV instance could be a .provn document, the result
of a query, a triple store containing PROV statements in RDF, etc. The
PROV-DM specification [PROV-DM] imposes minimal requirements upon
PROV instances. A valid PROV instance corresponds to a
consistent history of objects and interactions to which logical
reasoning can be safely applied. By default, PROV instances need not
be valid.
This document specifies inferences over PROV instances
that applications may employ, including definitions of some
provenance statements in terms of others, and also defines a class of
valid PROV instances by specifying constraints that
valid PROV instances must satisfy. Applications should produce valid
provenance and may reject provenance that is not valid. Applications
should also use definitions, inferences and constraints to normalize
PROV instances in order to determine whether two such instances convey
the same information.
To summarize: compliant applications use definitions,
inferences, and uniqueness constraints to normalize PROV instances,
and then apply event ordering constraints to determine whether the
instance has a consistent event ordering. If so, the instance is
valid, and the normal form is considered equivalent to
the original instance. Also, any two PROV instances that yield the
same normal form are considered equivalent. Further discussion
of the semantics of PROV statements, which justifies the inferences
and constraints, can be found in the formal semantics [PROV-SEM].
1.3 Structure of this document
Section 2 gives a brief rationale
for the definitions, inferences and constraints.
Section 3 summarizes the
requirements for compliance with this document, which are specified in
detail in the rest of the document.
Section 4 presents inferences and
definitions. Definitions allow replacing shorthand notation in [PROV-N]
with more explicit and complete statements; inferences allow adding
new facts representing implicit knowledge about the structure of
provenance.
Section 5 presents three kinds of constraints,
uniqueness constraints that prescribe that certain statments
must be unique within PROV instances,
event ordering constraints that require that the records in a
PROV instance are consistent with a sensible ordering of events
relating the activities, entities and agents involved, and
impossibility constraints that forbid certain patterns of
statements in valid PROV instances.
Section 6 defines the notions
of validity, equivalence and normalization.
1.4 Audience
The audience for this document is the same as for [PROV-DM]: developers
and users who wish to create, process, share or integrate provenance
records on the (Semantic) Web. Not all PROV-compliant applications
need to perform inferences or check validity when processing provenance.
However, applications that create or transform provenance should
attempt to produce valid provenance, to make it more useful to other
applications by ruling out nonsensical or inconsistent information.
This document assumes familiarity with [PROV-DM] and employs the
[PROV-N] notation.
2. Rationale
This section is non-normative.
In this section we give a high-level rationale that provides some
further background for the constraints.
2.1 Entities, Activities and Agents
One of the central challenges in representing provenance information
is how to deal with change. Real-world objects, information objects
and Web resources change over time, and the characteristics that make
them identifiable in a given situation are sometimes subject to change
as well. To avoid over-reliance on assumptions that identifying
characteristics do not change, PROV allows for things to be described
in different ways, with different descriptions of their partial
state.
An entity is a thing one wants to provide provenance for
and whose situation in the world is described by some fixed
attributes. An entity has a lifetime,
defined as the period
between its generation event
and its invalidation event.
An entity's attributes are established when the entity is
created and describe the entity's situation and (partial) state
during an entity's lifetime.
A different entity (perhaps representing a different user or
system perspective) may fix other aspects of the same thing, and its provenance
may be different. Different entities that are aspects of the same
thing are called alternate, and the PROV relations of
specialization and alternate can be used to link such entities.
Besides entities, a variety of other PROV objects have
attributes, including activity, generation, usage, invalidation, start, end,
communication, attribution, association, delegation, and
derivation. Each object has an associated duration interval (which may
be a single time point), and attribute-value pairs for a given object
are expected to be descriptions that hold for the object's duration.
However, the attributes of entities have special meaning because they
are considered to be fixed aspects
of underlying, changing things. This motivates constraints on
alternateOf and specializationOf relating the attribute values of
different entities.
In order to describe the provenance of something during an interval
over which relevant attributes of the thing are not fixed, a PROV
instance would describe multiple entities, each with its own
identifier, lifetime, and fixed attributes, and express dependencies between
the various entities using events. For example, if we want to
describe the provenance of several versions of a document, involving
attributes such as authorship that change over time, we need
different entities for the versions linked by appropriate
generation, usage, revision, and invalidation events.
There is no assumption that the set of attributes listed in an
entity statement is complete, nor
that the attributes are independent or orthogonal of each
other. Similarly, there is no assumption that the attributes of an
entity uniquely identify it. Two different entities that present the
same aspects of possibly different things can have the same
attributes; this leads to potential ambiguity, which is mitigated through the
use of identifiers.
An activity is delimited by its start and its end events; hence, it occurs over
an interval delimited by two instantaneous
events. However, an activity statement need not mention start or end time information, because they may not be known.
An activity's attribute-value pairs are expected to describe the activity's situation during its interval, i.e. an interval between two instantaneous events, namely its start event and its end event.
An activity is not an entity. Indeed, an entity exists in full at
any point in its lifetime, persists during this interval, and
preserves the characteristics that make it identifiable. In
contrast, an activity is something that occurs, happens, unfolds, or
develops through time, but is typically not identifiable by the
characteristics it exhibits at any point during its duration. This
distinction is similar to the distinction between 'continuant' and
'occurrent' in logic [Logic].
2.2 Events
Although time is important for provenance, provenance can be used
in many different contexts within individual systems and across the
Web. Different systems may use different clocks which may not be
precisely synchronized, so when provenance statements are combined by
different systems, we may not be able to align the times involved to a
single global timeline. Hence, PROV is designed to minimize
assumptions about time. Instead, PROV talks about (identified)
events.
The PROV data model is implicitly based on a notion of instantaneous events (or just events), that mark
transitions in the world. Events include generation, usage, or
invalidation of entities, as well as start or end of activities. This
notion of event is not first-class in the data model, but it is useful
for explaining its other concepts and its semantics [PROV-SEM].
Thus, events help justify inferences on provenance as well as
validity constraints indicating when provenance is
self-consistent.
Five kinds of instantaneous
events are used in PROV. The activity start
and activity end events delimit the beginning and the
end of activities, respectively. The entity usage,
entity generation, and entity
invalidation events apply to entities, and the generation and
invalidation events delimit the lifetime of an entity. More
precisely:
An activity start event is the instantaneous event that marks the instant an activity starts.
An activity end event is the instantaneous event that marks the instant an activity ends.
An entity usage event is the instantaneous event that marks the first instant of
an entity's consumption timespan by an activity. Before this instant
the entity had not begun to be used by the activity.
An entity generation event is the instantaneous event that marks the final instant of an entity's creation timespan, after which
it is available for use. The entity did not exist before this event.
An entity invalidation event
is the instantaneous event that
marks the initial instant of the destruction, invalidation, or
cessation of an entity, after which the entity is no longer available
for use. The entity no longer exists after this event.
2.3 Summary of constraints and inferences
Table 5 summarizes the definitions, inferences, and
constraints of this document.
Table: work in progress; these entries might change when the document is updated.
4. Inferences and Definitions
In this section, we describe inferences and definitions that may be used on
provenance data, and preserve equivalence on valid
PROV instances (as detailed in section 6. Normalization, Validity, and Equivalence).
An inference is a rule that can be applied
to PROV instances to add new PROV statements. A definition is a rule that states that a
provenance statement is equivalent to some other statements; thus,
defined provenance statements can be replaced by their definitions,
and vice versa.
Inferences have the following general form:
IF hyp1 and ... and
hypk THEN
there exists a1 and ... and am such that conclusion1 and ... and conclusionn.
This means that if all of the provenance statements matching
hyp1... hypk
can be found in a PROV instance, we can add all of the statements
concl1 ... concln to the instance, possibly after
generating fresh identifiers a1,...,am for unknown objects. These fresh
identifiers might later be found to be equal to known identifiers;
they play a similar role in PROV constraints to existential
variables in logic, "labeled nulls" in database theory [DBCONSTRAINTS], or to blank nodes in [RDF]. With a few
exceptions (discussed below), omitted optional parameters to
[PROV-N] statements, or explicit -
markers, are placeholders for existentially quantified variables;
that is, they denote unknown values.
Definitions have the following general form:
defined_exp holds IF AND ONLY IF
there exists a1,..., am such that defining_exp1 and ... and defining_expn.
This means that a provenance statement defined_exp is defined in
terms of other statements. This can be viewed as a two-way
inference: If defined_exp
can be found in a PROV instance, we can add all of the statements
defining_exp1 ... defining_expn to the instance, possibly after generating fresh
identifiers a1,...,am for unknown objects. It is safe to replace
a defined statement with
its definition.
Definitions and inferences can be viewed as logical formulas;
similar formalisms are often used in rule-based reasoning [CHR]
and in databases [DBCONSTRAINTS]. In particular, the identifiers
a1 ... an
should be viewed as existentially quantified variables, meaning that
through subsequent reasoning steps they may turn out to be equal to
other identifiers that are already known, or to other existentially
quantified variables. Their treatment is analogous to that of blank
nodes in RDF. In contrast, distinct URIs or literal values in PROV
are assumed to be distinct for the purpose of checking validity or
inferences. This issue is discussed in more detail under Uniqueness Constraints below.
4.1 Optional Identifiers and Attributes
Many PROV relation statements have an identifier, identifying a
link between two or more related objects. Identifiers can sometimes
be omitted in [PROV-N] notation. For the purpose of inference and
validity checking, we generate special identifiers called
existential variables denoting the unknown values.
Existential variables can be substituted with constant
identifiers, literals, the placeholder -,
or other existential variables.
We note that Definitions 1, 2, and 3 desugar compact PROV-N notation into a normal form.
For each r in {
used,
wasGeneratedBy,
wasInvalidatedBy,
wasInfluencedBy,
wasStartedBy,
wasEndedBy,
wasInformedBy,
wasDerivedFrom,
wasAttributedTo,
wasAssociatedWith,
actedOnBehalfOf}, the following
definitional rules hold:
-
r(a1,...,an) holds IF AND ONLY IF
there exists id such that r(id;a1,...,an) holds.
- r(-;a1,...,an) holds IF AND ONLY IF
there exists id such that r(id;a1,...,an) holds.
Likewise, many PROV statements allow for an optional attribute
list. If it is omitted, this is the same as specifying an empty
attribute list:
-
For each r in {entity, activity,
agent}, if a_n is not an attribute
list parameter then the following definitional rule holds:
r(a1,...,an)
holds IF AND ONLY IF r(a1,...,an,[]) holds.
-
For each r in {
used,
wasGeneratedBy,
wasInvalidated,
wasInfluencedBy,
wasStartedBy,
wasEndedBy,
wasInformedBy,
wasDerivedFrom,
wasAttributedTo,
wasAssociatedWith,
actedOnBehalfOf}, if a_n is not an
attribute list parameter then the following definition holds:
r(id;a1,...,an) holds
IF AND ONLY IF r(id;a1,...,an,[]) holds.
Finally, many PROV
statements have other optional arguments or short forms that can be
used if none of the optional arguments is present. These are
handled by specific rules listed below.
Finally, most optional parameters (written -) are, for the purpose of this document,
considered to be distinct, fresh existential variables. Thus,
before proceeding to apply other definitions or inferences, most
occurrences of - must be replaced
by fresh existential variables, distinct from any others occurring in
the instance.
The only exceptions, where - must be left
in place, are the activity parameter in wasDerivedFrom and
the plan parameter in wasAssociatedWith.
The following table characterizes the expandable
parameters of the properties of PROV, needed in the
following definition. For emphasis, the two optional parameters
that are not expandable are
also listed.
| | |
| Relation |
Expandable |
Non-expandable |
| wasGeneratedBy(id;e,a,t,attrs) |
id,a,t |
|
| used(id;a,e,t,attrs) |
id,e,t |
|
| wasInformedBy(id;a2,a1,attrs) |
id |
|
| wasStartedBy(id;a2,e,a1,t,attrs) |
id,e,a1,t |
|
| wasEndedBy(id;a2,e,a1,t,attrs) |
id,e,a1,t |
|
| wasInvalidatedBy(id;e,a,t,attrs) |
id,a,t |
|
| wasDerivedFrom(id;e2,e1,a,g2,u1,attrs) |
id,g2,u1 |
a |
| wasDerivedFrom(id;e2,e1,attrs) |
id |
|
| wasAttributedTo(id;e,ag,attr) |
id |
|
| wasAssociatedWith(id;a,ag,pl,attrs) |
id,ag |
pl |
| actedOnBehalfOf(id;ag2,ag1,a,attrs) |
id,a |
|
| wasInfluencedBy(id;e2,e1,attrs) |
id |
|
-
For each r in {entity, activity,
agent}, the following definition
holds:
r(a0,...,ai-1, -, ai+1, ...,an) IF AND ONLY IF there exists a'
such that r(a0,...,ai-1,a',ai+1,...,an).
- For each r in {
used,
wasGeneratedBy,
wasInfluencedBy,
wasInvalidatedBy,
wasStartedBy,
wasEndedBy,
wasInformedBy,
wasDerivedFrom,
wasAttributedTo,
wasAssociatedWith,
actedOnBehalfOf}, if the ith parameter
of r is an expandable parameter
of r then the following definition holds:
r(a0;...,ai-1, -, ai+1, ...,an) IF AND ONLY IF there exists a'
such that r(a0;...,ai-1,a',ai+1,...,an).
4.2 Entities and Activities
Communication between activities is defined as the existence of an underlying
entity generated by one activity and used by the other.
IF
wasInformedBy(_id;a2,a1,_attrs)
holds THEN
there exist e, _id1, _t1, _id2, and _t2,
such that wasGeneratedBy(_id1;e,a1,_t1,[]) and used(_id2;a2,e,_t2,[]) hold.
IF wasGeneratedBy(_id1;e,a1,_t1,_attrs1)
and used(_id2;a2,e,_t2,_attrs2) hold
THEN
there exists _id
such that wasInformedBy(_id;a2,a1,[])
From an entity, we can infer that existence of
generation and invalidation events.
IF entity(e,_attrs) THEN there exist
_id1, _a1, _t1,
_id2, _a2, and _t2 such that
wasGeneratedBy(_id1;e,_a1,_t1,[]) and wasInvalidatedBy(_id2;e,_a2,_t2,[]).
From an activity statemen,t we can infer that
start and end events having times matching the start and end times of
the activity.
IF activity(a,t1,t2,_attrs) THEN there exist _id1, _e1, _id2,
and _e2 such that
wasStartedBy(_id1;a,_e1,_a1,t1,[]) and wasEndedBy(_id2;a,_e2,_a2,t2,[]).
Start of a by trigger e1 and starter activity a1 implies that
e1 was generated by a1.
IF
wasStartedBy(_id;a,e1,a1,_t,_attrs),
THEN there exist _gen and _t1
such that
wasGeneratedBy(_gen;e1,a1,_t1,[]).
Likewise,
end of a by trigger e1 and ender activity a1 implies that
e1 was generated by a1.
IF
wasEndedBy(_id;a,e1,a1,_t,_attrs),
THEN there exist _gen and _t1 such that
wasGeneratedBy(_gen;e1,a1,_t1,[]).
4.3 Derivations
Derivations with explicit
activity, generation, and usage admit the following inference:
IF wasDerivedFrom(_id;e2,e1,a,id2,id1,_attrs),
THEN there exists _t1 and _t2 such that used(id1;a,e1,_t1,[]) and wasGeneratedBy(id2;e2,a,_t2,[]) hold.
Derivations with an explicit activity and
no specified generation and usage admit the following inference:
Final check required. The following inference
appears redundant (it can be derived using other rules).
IF wasDerivedFrom(id;e2,e1,a,-,-,attrs) and wasGeneratedBy(gen;e2,a,_t2,_attrs2) hold, THEN there exist _t1 and use such
that used(use;a,e1,_t1,[]) and wasDerivedFrom(id;e2,e1,a,gen,use,attrs) hold.
This inference is justified by the fact that the entity denoted by e2 is generated by at most one activity
(see Constraint 27 (unique-generation)). Hence, this activity is also the one referred to by the usage of e1.
A derivation
specifying activity, generation and use events is a special case of
a derivation that leaves these unspecified. (The converse is not
the case).
IF wasDerivedFrom(id;e2,e1,_act,_gen,_use,attrs)
holds, THEN wasDerivedFrom(id;e2,e1,-,-,-,attrs) holds.
A revision admits the following inference, stating that the two entities
linked by a revision are also alternates.
IF wasDerivedFrom(_id;e2,e1,[prov:type='prov:Revision'])
holds, THEN alternateOf(e2,e1) holds.
4.4 Agents
Attribution identifies an agent as responsible for an entity. An
agent can only be responsible for an entity if it was associated with
an activity that generated the entity. If the activity, generation
and association events are not explicit in the instance, they can
be inferred.
IF
wasAttributedTo(_att;e,ag,_attrs) holds for some identifiers
e and ag,
THEN there exist
a,
_t,
_gen,
_assoc,
_pl,
such that
wasGeneratedBy(_gen;e,a,_t,[]) and
wasAssociatedWith(_assoc;a,ag,_pl,[]) hold.
Delegation relates agents where one agent acts on behalf of
another, in the context of some activity. The supervising agent
delegates some responsibility for part of the activity to the
subordinate agent, while retaining some responsibility for the overall
activity. Both agents are associated with this activity.
IF
actedOnBehalfOf(_id;ag1, ag2, a, _attrs)
THEN there exist _id1, _pl1, _id2, and _pl2 such that wasAssociatedWith(_id1;a, ag1, _pl1, [])
and wasAssociatedWith(_id2;a, ag2, _pl2, []).
The wasInfluencedBy relation is implied by other relations, including
usage, start, end, generation, invalidation, communication,
derivation, attribution, association, and delegation. To capture this
explicitly, we allow the following inferences:
-
IF wasGeneratedBy(id;e,a,t,attrs) THEN wasInfluencedBy(id; e, a, attrs).
-
IF used(id;a,e,t,attrs) THEN wasInfluencedBy(id; a, e, attrs).
-
IF wasInformedBy(id;a2,a1,attrs) THEN wasInfluencedBy(id; a2, a1, attrs).
-
IF wasStartedBy(id;a2,e,a1,t,attrs) THEN wasInfluencedBy(id; a2, e, attrs).
-
IF wasEndedBy(id;a2,e,a1,t,attrs) THEN wasInfluencedBy(id; a2, e, attrs).
-
IF wasInvalidatedBy(id;e,a,t,attrs) THEN wasInfluencedBy(id; e, a, attrs).
-
IF wasDerivedFrom(id; e2, e1, attrs) THEN wasInfluencedBy(id; e2, e1, attrs).
-
IF wasAttributedTo(id;e,ag,attr) THEN wasInfluencedBy(id; e, ag, attrs).
-
IF wasAssociatedWith(id;a,ag,pl,attrs) THEN wasInfluencedBy(id; a, ag, attrs).
-
IF actedOnBehalfOf(id;ag2,ag1,a,attrs) THEN wasInfluencedBy(id; ag2, ag1, attrs).
4.5 Alternate and Specialized Entities
The relation alternateOf is an equivalence relation: reflexive,
transitive and symmetric.
For any entity e, we have alternateOf(e,e).
IF alternateOf(e1,e2) and
alternateOf(e2,e3) THEN alternateOf(e1,e3).
IF alternateOf(e1,e2) THEN alternateOf(e2,e1).
Similarly, specialization is a
strict partial order: it is irreflexive and
transitive. Irreflexivity is handled later as a
constraint.
IF specializationOf(e1,e2)
and
specializationOf(e2,e3) THEN specializationOf(e1,e3).
If one entity specializes another, then they are also
alternates:
IF specializationOf(e1,e2) THEN alternateOf(e1,e2).
If one entity specializes another then all attributes of the more
general entity are also attributes of the more specific one.
IF entity(e1, attrs) holds for some
attributes attrs and specializationOf(e2,e1) holds, THEN
entity(e2, attrs) also holds.
Note: The following inference is associated with a feature "at risk" and may be removed from this specification based on feedback. Please send feedback to public-prov-comments@w3.org.
If one entity is a mention of another in a bundle, then the former is also a specialization of the latter:
IF mentionOf(e2,e1,b) THEN specializationOf(e2,e1).
5. Constraints
This section defines a collection of constraints on PROV instances.
There are three kinds of constraints:
- uniqueness constraints that say that a PROV
instance can contain at most one statement of each kind with a
given identifier. For
example, if we describe the same generation event twice, then the
two statements should have the same times;
- event ordering constraints that say that it
should be possible to arrange the
events (generation, usage, invalidation, start, end) described in a
PROV instance into a preorder that corresponds to a sensible
"history" (for example, an entity should not be generated after it
is used); and
- impossibility constraints, which forbid certain
patterns of statements in valid PROV instances.
5.1 Uniqueness Constraints
In the absence of existential variables, uniqueness constraints
could be checked directly by checking that no identifier appears
more than once for a given statement. However, in the presence of
existential variables, we need to be more careful to combine
partial information that might be present in multiple compatible
statements, due to inferences. Uniqueness constraints are
enforced through merging pairs of statements subject to
equalities. For example, suppose we have two activity statements
activity(a,2011-11-16T16:00:00,t1,[a=1]) and activity(a,t2,2011-11-16T18:00:00,[b=2]). The merge of
these two statements (describing the same activity a) is activity(a,2011-11-16T16:00:00,2011-11-16T18:00:00,[a=1,b=2]).
Merging can be applied
to a pair of terms, or a pair of attribute lists.
The result of merging is either a substitution (mapping
existentially quantified variables to terms) or a special symbol
undefined indicating that the merge
cannot be performed. Merging of pairs of terms, attribute lists,
or statements is defined as follows.
- If t and t' are concrete identifiers or values
(including the placeholder -), then
their merge exists only if they are equal, otherwise merging
is undefined.
- If x is an existential variable
and
t' is any term (identifier, constant,
placeholder -, or
existential variable), then their
merge is t', and the resulting substitution is
[x=t']. In the special case where t'=x, the merge is
x and the resulting substitution is empty.
- If t is any term (identifier, constant,
placeholder -, or
existential variable) and
x' is an existential variable, then their
merge is the same as the merge of x and t.
- The merge of two attribute lists attrs1 and attrs2
is their union, considered as unordered lists, written attrs1 ∪ attrs2.
A typical uniqueness constraint is as follows:
IF hyp1 and ... and hypn THEN t1 = u1 and ... and tn = un.
Such a constraint is enforced as follows:
- Suppose PROV instance I contains all of the hypotheses
hyp1 and ... and hypn.
- Attempt to merge all of the equated terms in the conclusion
t1 = u1 and ... and tn = un.
- If merging fails, then the constraint
is unsatisfiable, so application of the constraint to I
fails.
- If merging succeeds with a substitution S, then
S is applied to the instance I, yielding result I(S).
In the common case that a particular field of a relation uniquely
determines the other fields, we call the uniqueness constraint a
key constraint. Key constraints are written as follows:
The ak field is a KEY for relation r(a0;a1,...,an).
Because of the presence of attributes, key constraints do not
reduce directly to uniqueness constraints. Instead, we enforce key
constraints as follows.
- Suppose r(a0;a1,...an,attrs1) and r(b0;b1,...bn,attrs2) hold in PROV instance I, where the key fields ak = bk are equal.
- Attempt to merge all of the corresponding parameters a0 = b0 and ... and an = bn.
- If merging fails, then the constraint is unsatisfiable, so
application of the key constraint to I fails.
- If merging succeeds with substitution S, then we remove r(a0;a1,...an,attrs1) and r(b0;b1,...bn,attrs2) from I, obtaining
instance I', and return instance {r(S(a0);S(a1),...S(an),attrs1 ∪
attrs2)} ∪ S(I').
Thus, if a PROV instance contains an apparent violation of a uniqueness
constraint or key constraint, merging can be used to determine
whether the constraint can be satisfied by instantiating some existential
variables with other terms. For key constraints, this is the same
as merging pairs of statements whose keys are equal and whose
coresponding arguments are compatible, because after
merging respective arguments and attribute lists, the two statements
become equal and one can be omitted.
We assume that the various identified objects of PROV have
unique statements describing them within a PROV instance, through
the following key constraints:
- The identifier field e is a KEY for
the entity(e,attrs) statement.
- The identifier field a is a KEY for
the activity(a,t1,t2,attrs) statement.
- The identifier field ag is a KEY for
the agent(ag,attrs) statement.
Likewise, we assume that the identifiers
of relationships in PROV uniquely identify the corresponding statements a PROV instance, through
the following key constraints:
- The identifier field id is a KEY for
the wasGeneratedBy(id;e,a,t,attrs) statement.
- The identifier field id is a KEY for
the used(id;a,e,t,attrs) statement.
- The identifier field id is a KEY for
the wasInformedBy(id;a2,a1,attrs) statement.
- The identifier field id is a KEY for
the wasStartedBy(id;a2,e,a1,t,attrs) statement.
- The identifier field id is a KEY for
the wasEndedBy(id;a2,e,a1,t,attrs) statement.
- The identifier field id is a KEY for
the wasInvalidatedBy(id;e,a,t,attrs) statement.
- The identifier field id is a KEY for
the wasDerivedFrom(id; e2, e1, attrs) statement.
- The identifier field id is a KEY for
the wasDerivedFrom(id; e2, e1, a, g2, u1, attrs) statement.
- The identifier field id is a KEY for
the wasAttributedTo(id;e,ag,attr) statement.
- The identifier field id is a KEY for
the wasAssociatedWith(id;a,ag,pl,attrs) statement.
- The identifier field id is a KEY for
the wasAssociatedWith(id;a,ag,-,attrs) statement.
- The identifier field id is a KEY for
the actedOnBehalfOf(id;ag2,ag1,a,attrs) statement.
- The identifier field id is a KEY for
the wasInfluencedBy(id;o2,o1,attrs) statement.
We assume that an entity has exactly one generation and
invalidation event (either or both may, however, be left implicit).
Note that together with the key constraints above, this implies that
e is also a key for generation and
invalidation statements.
IF wasGeneratedBy(id1;e,_a1,_t1,_attrs1) and wasGeneratedBy(id2;e,_a2,_t2,_attrs2),
THEN id1=id2.
IF wasInvalidatedBy(id1;e,_a1,_t1,_attrs1) and wasInvalidatedBy(id2;e,_a2,_t2,_attrs2),
THEN id1=id2.
It follows from the above constraints that the generation and
invalidation times of
an entity are unique, if specified.
We assume that an activity has exactly one start and
end event (either or both may, however, be left implicit). Again,
together with above key constraints these constraints imply that the
activity is a key for activity start and end statements.
IF wasStartedBy(id1;a,_e1,_a1,_t1,_attrs1) and wasStartedBy(id2;a,_e2,_a2,_t2,_attrs2), THEN id=id'.
IF wasEndedBy(id1;a,_e1,_a1,_t1,_attrs1) and wasEndedBy(id2;a,_e2,_a2,_t2,_attrs2), THEN id=id'.
An activity start event is the instantaneous event that marks the instant an activity starts. It allows for an optional time attribute. Activities also allow for an optional start time attribute. If both are specified, they must be the same, as expressed by the following constraint.
IF activity(a,t,_t',_attrs) and wasStartedBy(id;a,_e1,_a1,t1,_attrs1), THEN t=t1.
An activity end event is the instantaneous event that marks the instant an activity ends. It allows for an optional time attribute. Activities also allow for an optional end time attribute. If both are specified, they must be the same, as expressed by the following constraint.
IF activity(a,_t,t',_attrs) and wasEndedBy(id;a,_e1,_a1,t1,_attrs1), THEN t' = t1.
Note: The following constraint is associated with a feature "at risk" and may be removed from this specification based on feedback. Please send feedback to public-prov-comments@w3.org.
An entity can be the subject of at most one mention relation.
IF mentionOf(e, e1, b1) and mentionOf(e, e2, b2),
THEN e1=e2 and b1=b2.
5.2 Event Ordering Constraints
Given that provenance consists of a description of past entities
and activities, valid provenance instances must
satisfy ordering constraints between instantaneous events, which we introduce in
this section. For instance, an entity can only be used after it was
generated; hence, we say that an entity's generation event precedes any of this
entity's usage events. Should this
ordering constraint be violated, the associated generation and
usage would not be credible. The rest of this section defines
the temporal interpretation of provenance instances as a
set of instantaneous event ordering constraints.
To allow for minimalistic clock assumptions, like Lamport
[CLOCK], PROV relies on a notion of relative ordering of instantaneous events,
without using physical clocks. This specification assumes that a preorder exists between instantaneous events.
Specifically, precedes is a preorder
between instantaneous events. When
we say e1 precedes e2, this means that e1
happened at the same time as or before e2.
For symmetry, follows is defined as the
inverse of precedes; that is, when we say
e1 follows e2,
this means that e1 happened at the same time
as or after e2. Both relations are
preorders, meaning that they are reflexive and
transitive. Moreover, we sometimes consider strict forms of these
orders: we say e1 strictly precedes e2 to indicate that e1
happened before e2. This is a
transitive relation.
PROV also allows for time observations to be inserted in
specific provenance statements, for each of the five kinds of instantaneous events introduced in
this specification. Times in provenance records arising from
different sources might be with respect to different timelines
(e.g. different time zones) leading to apparent inconsistencies. For
the purpose of checking ordering constraints, the times associated
with events are irrelevant; thus, there is no inference that time ordering
implies event ordering, or vice versa. However, an application may flag time values
that appear inconsistent with the event ordering as possible
inconsistencies. When generating provenance, an application should
use a consistent timeline for related PROV statements within an
instance.
A typical ordering constraint is as follows.
The conclusion of an ordering constraint is either precedes
or strictly precedes. To check ordering constraints, we
generate all precedes and strictly
precedes
relationships arising from the ordering constraints to form a directed graph, with edges marked precedes or
strictly precedes, and check that there is no cycle
containing a strictly precedes edge.
5.2.1 Activity constraints
In this section we discuss constraints from the perspective of
the lifetime of an activity. An activity starts, then during
its lifetime uses, generates or invalidates entities, and communicates with or starts
other
activities, and finally ends. The following constraints amount to
checking that all of the events associated with an activity take place
within the activity's lifetime, and the start and end events mark the
start and endpoints of its lifetime.
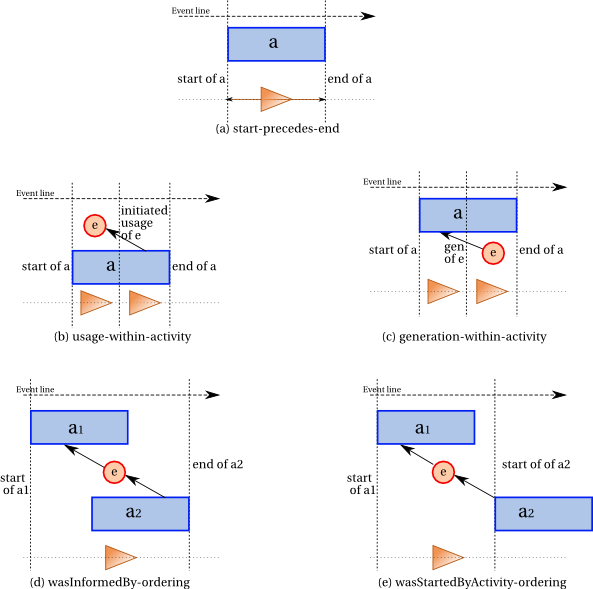
Figure 2 summarizes the ordering
constraints on activities in a
graphical manner. For this and subsequent figures, an event time line points to the
right. Activities are represented by rectangles, whereas entities are
represented by circles. Usage, generation and invalidation are
represented by the corresponding edges between entities and
activities. The five kinds of instantaneous events are represented by vertical
dotted lines (adjacent to the vertical sides of an activity's
rectangle, or intersecting usage and generation edges). The ordering
constraints are represented by triangles: an occurrence of a triangle between two instantaneous event vertical dotted lines represents that the event denoted by the left
line precedes the event denoted by the right line.
Miscellanous suggestions about figures
(originally from Tim Lebo):
-
I think it would help if the "corresponding edges between entities and activities" where the same visual style as the vertical line marking the time the Usage, generation and derivation occurred. A matching visual style provides a Gestalt that matches the concept. I am looking at subfigures b and c in 5.2.
The existence of an activity implies that the activity start
event always precedes the corresponding activity end
event. This is illustrated by
Figure 2
(a) and expressed by Constraint 34 (start-precedes-end).
IF
wasStartedBy(start;a,_e1,_a1,_t1,_attrs1)
and
wasEndedBy(end;a,_e2,_a2,_t2,_attrs2)
THEN
start
precedes
end.
A usage implies ordering of events, since the usage event had to occur during the associated activity. This is
illustrated by Figure 2 (b) and expressed by Constraint 35 (usage-within-activity).
-
IF
used(use;a,e,_t,_attrs)
and
wasStartedBy(start;a,_e1,_a1,_t1,_attrs1)
THEN
start
precedes
use.
-
IF
used(use;a,e,_t,_attrs)
and
wasEndedBy(end;a,_e1,_a1,_t1,_attrs1)
THEN
use
precedes
end.
A generation implies ordering of events, since the generation event had to occur during the associated activity. This is
illustrated by Figure 2 (c) and expressed by Constraint 36 (generation-within-activity).
-
IF
wasGeneratedBy(gen;_e,a,_t,_attrs)
and
wasStartedBy(start;a,_e1,_a1,_t1,_attrs1)
THEN
start
precedes
gen.
-
IF
wasGeneratedBy(gen;_e,a,_t,_attrs)
and
wasEndedBy(end;a,_e1,_a1,_t1,_attrs1)
THEN
gen
precedes
end.
Communication between two activities a1
and a2 also implies ordering
of events, since some entity must
have been generated by the former and used by the latter, which
implies that the start event of a1 cannot
follow the end event of a2. This is
illustrated by
Figure 2
(d) and expressed by Constraint 37 (wasInformedBy-ordering).
5.2.2 Entity constraints
The figure(s) in this section should have vertical lines with visual styles that match the diagonal arrow that they go with.
As with activities, entities have lifetimes: they are generated, then
can be used, revised, or other entities can be derived from them, and
finally they may be invalidated. The constraints on these events are
illustrated graphically in Figure 3 and
Figure 4.
Generation of an entity precedes its invalidation. (This
follows from other constraints if the entity is used, but we state it
explicitly to cover the case of an entity that is generated and
invalidated without being used.)
IF
wasGeneratedBy(gen;e,_a1,_t1,_attrs1)
and
wasInvalidatedBy(inv;e,_a2,_t2,_attrs2)
THEN
gen
strictly precedes
inv.
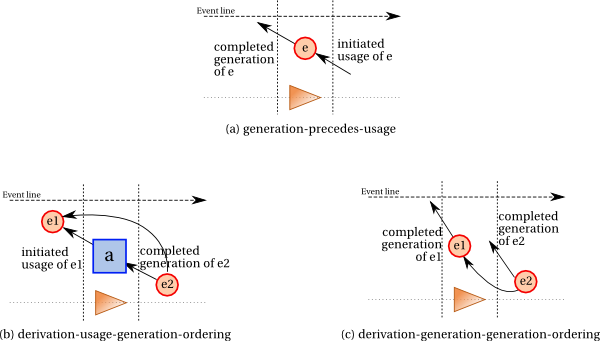
A usage and a generation for a given entity implies ordering of events, since the generation event had to precede the usage event. This is
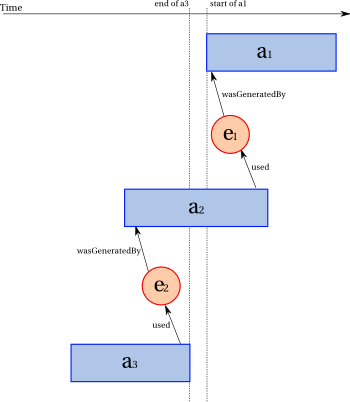
illustrated by Figure 3(a) and expressed by Constraint 39 (generation-precedes-usage).
IF
wasGeneratedBy(gen;e,_a1,_t1,_attrs1)
and
used(use;_a2,e,_t2,_attrs2)
THEN
gen
precedes
use.
All usages of an entity precede its invalidation, which is captured by Constraint 40 (usage-precedes-invalidation) (without any explicit graphical representation).
IF
used(use;_a1,e,_t1,_attrs1)
and
wasInvalidatedBy(inv;e,_a2,_t2,_attrs2)
THEN
use
precedes
inv.
If there is a
derivation relationship linking e2 and e1, then
this means that the entity e1 had some influence on the entity e2; for this to be possible, some event ordering must be satisfied.
First, we consider derivations, where the activity and usage are known. In that case, the usage of e1 has to precede the generation of e2.
This is
illustrated by Figure 3 (b) and expressed by Constraint 41 (derivation-usage-generation-ordering).
When the activity, generation or usage is unknown, a similar constraint exists, except that the constraint refers to its
generation event, as
illustrated by Figure 3 (c) and expressed by Constraint 42 (derivation-generation-generation-ordering).
IF
wasDerivedFrom(_d;e2,e1,attrs)
and
wasGeneratedBy(gen1;e1,_a1,_t1,_attrs1)
and
wasGeneratedBy(gen2;e2,_a2,_t2,_attrs2)
THEN
gen1
strictly precedes
gen2.
Note that event ordering is between generations of e1
and e2, as opposed to derivation where usage is known,
which implies ordering between the usage of e1 and
generation of e2.
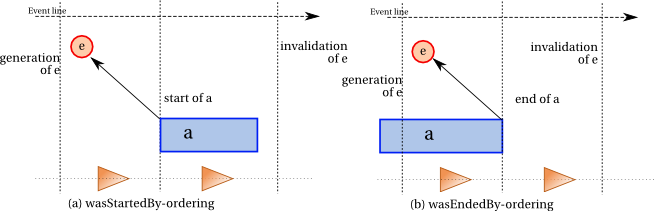
The entity that triggered the start of an activity must exist before the activity starts.
This is
illustrated by Figure 4(a) and expressed by Constraint 43 (wasStartedBy-ordering).
-
IF
wasStartedBy(start;_a,e,_a1,_t1,_attrs1)
and
wasGeneratedBy(gen;e,_a2,_t2,_attrs2)
THEN
gen
precedes
start.
-
IF
wasStartedBy(start;_a,e,_a1,_t1,_attrs1)
and
wasInvalidatedBy(inv;e,_a2,_t2,_attrs2)
THEN
start
precedes
inv.
Similarly, the entity that triggered
the end of an activity must exist before the activity ends, as
illustrated by
Figure 4(b).
-
IF
wasEndedBy(end;_a,e,_a1,_t1,_attrs1)
and
wasGeneratedBy(gen;e,_a2,_t2,_attrs2)
THEN
gen
precedes
end.
-
IF
wasEndedBy(end;_a,e,_a1,_t1,_attrs1)
and
wasInvalidatedBy(inv;e,_a2,_t2,_attrs2)
THEN
end
precedes
inv.
If an entity specalizes another, then its generation must follow the
specialized entity's generation.
IF specializationOf(e2,e1) and wasGeneratedBy(gen1;e1,_a1,_t1,_attrs1) and
wasGeneratedBy(gen2;e2,_a2,_t2,_attrs2)
THEN gen1 precedes gen2.
Similarly, if an entity specalizes another, then its invalidation must follow the
specialized entity's invalidation.
IF specializationOf(e2,e1) and wasInvalidatedBy(inv1;e1,_a1,_t1,_attrs1) and
wasInvalidatedBy(inv2;e2,_a2,_t2,_attrs2)
THEN inv2 precedes inv1.
5.2.3 Agent constraints
Like entities and activities, agents have lifetimes that follow a
familiar pattern: an agent is generated, can participate in
interactions such as starting, ending or association with an
activity, attribution, or delegation, and finally the agent is invalidated.
Further constraints associated with agents appear in Figure 5 and are discussed below.
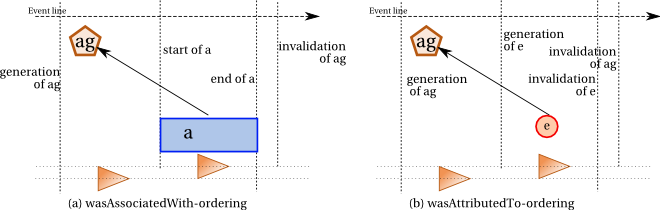
An activity that was associated with an agent must have some overlap with the agent. The agent may be generated, or may only become associated with the activity, after the activity start: so, the agent is required to exist before the activity end. Likewise, the agent may be destructed, or may terminate its association with the activity, before the activity end: hence, the agent invalidation is required to happen after the activity start.
This is
illustrated by Figure 5 (a) and expressed by Constraint 47 (wasAssociatedWith-ordering).
-
IF
wasAssociatedWith(_assoc;a,ag,_pl,_attrs)
and
wasStartedBy(start;a,_e1,_a1,_t1,_attrs1)
and
wasInvalidatedBy(inv;ag,_a2,_t2,_attrs2)
THEN
start
precedes
inv.
-
IF
wasAssociatedWith(_assoc;a,ag,_pl,_attrs)
and
wasGeneratedBy(gen;ag,_a1,_t1,_attrs1)
and
wasEndedBy(end;a,_e2,_a2,_t2,_attrs2)
THEN
gen
precedes
end.
An entity that was attributed to an agent must have some overlap
with the agent. The agent is required to exist before the entity
invalidation. Likewise, the entity generation must precede the agent destruction.
This is
illustrated by Figure 5 (b) and expressed by Constraint 48 (wasAttributedTo-ordering).
-
IF
wasAttributedTo(_at;e,ag,_attrs)
and
wasGeneratedBy(gen;e,_a1,_t1,_attrs1)
and
wasInvalidatedBy(inv;ag,_a2,_t2,_attrs2)
THEN
gen
precedes
inv.
-
IF
wasAttributedTo(_at;e,ag,_attrs)
and
wasGeneratedBy(gen;ag,_a1,_t1,_attrs1)
and
wasInvalidatedBy(inv;e,_a2,_t2,_attrs2)
THEN
gen
precedes
inv.
For delegation, two agents need to have some overlap in their lifetime.
IF
actedOnBehalfOf(_del;ag2,ag1,_a,_attrs)
and
wasGeneratedBy(gen;ag1,_a1,_t1,_attrs1)
and
wasInvalidatedBy(inv;ag2,_a2,_t2,_attrs2)
THEN
gen
precedes
inv.
5.3 Impossibility constraints
Impossibility constraints require that certain patterns of
statements never appear in valid PROV instances. Impossibility
constraints have the following general form:
IF hyp1 and ... and hypn THEN INVALID.
To check an impossibility constraint on instance I, we check whether there is
any way of matching the pattern hyp1, ..., hypn. If there
is, then checking the constraint on I fails (which implies that
I is invalid).
Influence is required to
be irreflexive, that is, it is impossible for something to
influence itself.
IF wasInfluencedBy(e,e) THEN INVALID.
As noted previously, specialization is a
strict partial order: it is irreflexive and
transitive.
IF specializationOf(e,e) THEN INVALID.
Furthermore, identifiers
of basic relationships are disjoint.
For each r and s
in {
used,
wasGeneratedBy,
wasInvalidatedBy,
wasStartedBy,
wasEndedBy,
wasInformedBy,
wasAttributedTo,
wasAssociatedWith,
actedOnBehalfOf} such that r and s
are different relations, the
following constraint holds:
IF r(id;a1,...,an) and s(id;b1,...,bn) THEN INVALID.
Identifiers of entities,
agents and activities cannot also be identifiers of properties.
For each r in entity, activity
or agent and for each s in {
used,
wasGeneratedBy,
wasInvalidatedBy,
wasInfluencedBy,
wasStartedBy,
wasEndedBy,
wasInformedBy,
wasDerivedFrom,
wasAttributedTo,
wasAssociatedWith,
actedOnBehalfOf}, the following
impossibility constraint holds:
IF r(id,a1,...,an) and
s(id;b1,...,bn) THEN INVALID.
5.4 Type Constraints
The following rule establishes types denoted by identifiers from their use within expressions.
For this, the function typeOf gives the set of types denoted by an identifier.
For example, typeOf(e) returns the set of types associated with identifier e. The function typeOf is not a term of PROV, but a construct introduced to validate PROV statements.
For any identifier id, typeOf(id) is a subset of {'entity', 'activity', 'agent', 'prov:Collection', 'prov:EmptyCollection'}.
For identifiers that do not have a type, typeOf gives the empty set.
To check if a PROV instance satisfies type constraints, one obtains the types of identifiers by application of
Constraint 54 (typing)
and check no impossibility results from rules
Constraint 55 (entity-activity-disjoint) and
Constraint 56 (membership-empty-collection).
-
IF
wasGeneratedBy(gen;e,a,t,attrs)
THEN
'entity' ∈ typeOf(e) AND
'activity' ∈ typeOf(a).
-
IF
entity(e,attrs)
THEN
'entity' ∈ typeOf(e).
-
IF
agent(ag,attrs)
THEN
'agent' ∈ typeOf(ag).
-
IF
activity(a,attrs)
THEN
'activity' ∈ typeOf(a).
-
IF
used(u;a,e,t,attrs)
THEN
'activity' ∈ typeOf(a) AND
'entity' ∈ typeOf(e).
-
IF
wasInformedBy(id;a2,a1,attrs)
THEN
'activity' ∈ typeOf(a2) AND
'activity' ∈ typeOf(a1).
-
IF
wasStartedBy(id;a2,e,a1,t,attrs)
THEN
'activity' ∈ typeOf(a2) AND
'entity' ∈ typeOf(e) AND
'activity' ∈ typeOf(a1).
-
IF
wasEndedBy(id;a2,e,a1,t,attrs)
THEN
'activity' ∈ typeOf(a2) AND
'entity' ∈ typeOf(e) AND
'activity' ∈ typeOf(a1).
-
IF
wasInvalidatedBy(id;e,a,t,attrs)
THEN
'entity' ∈ typeOf(e) AND
'activity' ∈ typeOf(a).
-
IF
wasDerivedFrom(id; e2, e1, a, g2, u1, attrs)
THEN
'entity' ∈ typeOf(e2) AND
'entity' ∈ typeOf(e1) AND
'activity' ∈ typeOf(a).
-
IF
wasAttributedTo(id;e,ag,attr)
THEN
'entity' ∈ typeOf(e) AND
'agent' ∈ typeOf(ag).
-
IF
wasAssociatedWith(id;a,ag,pl,attrs)
THEN
'activity' ∈ typeOf(a) AND
'agent' ∈ typeOf(ag) AND
'entity' ∈ typeOf(pl).
-
IF
actedOnBehalfOf(id;ag2,ag1,a,attrs)
THEN
'agent' ∈ typeOf(ag2) AND
'agent' ∈ typeOf(ag1) AND
'activity' ∈ typeOf(a).
-
IF
alternateOf(e2, e1)
THEN
'entity' ∈ typeOf(e2) AND
'entity' ∈ typeOf(e1).
-
IF
specializationOf(e2, e1)
THEN
'entity' ∈ typeOf(e2) AND
'entity' ∈ typeOf(e1).
-
IF
mentionOf(e2,e1,b)
THEN
'entity' ∈ typeOf(e2) AND
'entity' ∈ typeOf(e1) AND
'entity' ∈ typeOf(b).
-
IF
hadMember(c,e)
THEN
'prov:Collection' ∈ typeOf(c) AND
'entity' ∈ typeOf(c) AND
'entity' ∈ typeOf(e).
-
IF
entity(c,[prov:type='prov:EmptyCollection'])
THEN
'entity' ∈ typeOf(c) AND
'prov:EmptyCollection' ∈ typeOf(c).
The set of entities and activities are disjoint, expressed by
the following constraint:
IF
'entity' ∈ typeOf(id) AND
'activity' ∈ typeOf(id)
THEN INVALID.
An empty collection cannot contain any member, expressed by
the following constraint:
IF
hasMember(c,e) and
'prov:EmptyCollection' ∈ typeOf(c)
THEN INVALID.
6. Normalization, Validity, and Equivalence
We define the notions of normalization, validity and
equivalence of PROV instances. We first define these concepts
for PROV instances that consist of a single, unnamed bundle of
statements, called the toplevel bundle.
We define the normal form of a PROV instance as the set
of provenance statements resulting from merging to resolve all
uniqueness constraints in the instance and applying all possible
inference rules to this set.
-
Apply all definitions to I by replacing each defined statement by its
definition (possibly introducing fresh existential variables in
the process), yielding an instance I1.
-
Apply all inferences to I1 by adding the conclusion of each inference
whose hypotheses are satisfied and whose entire conclusions do not
already hold (again, possibly introducing fresh existential
variables), yielding an instance I2.
-
Apply all uniqueness constraints to I2 by merging terms or statements
and applying the resulting substitution to the instance, yielding
an instance I3. If some uniqueness constraint cannot be
applied, then normalization fails.
- If no definitions, inferences, or uniqueness constraints can be applied to instance I3, then I3 is the
normal form of I.
- Otherwise, the normal form of I is the same as the normal form
of I3 (that is, proceed by recursively normalizing I3).
Because of the potential interaction among inferences, definitions and
constraints, the above algorithm is recursive. Nevertheless,
all of our constraints fall into a class of tuple-generating
dependencies and equality-generating dependencies that
satisfy a termination condition called weak acyclicity that
has been studied in the context of relational databases
[DBCONSTRAINTS]. Therefore, the above algorithm terminates, independently
of the order in which inferences and constraints are applied.
Appendix C gives a proof that normalization terminates and produces
a unique (up to isomorphism) normal form.
A PROV instance is valid
if its normal form exists and satisfies all of
the validity constraints; this implies that the instance satisfies
all of the inferences, definitions and constraints.
The following algorithm can be used to test
validity:
- Normalize the instance, obtaining normalized instance I'. If
normalization fails, then I is not valid.
- Apply all event ordering constraints to I' to build a graph G whose nodes
are event identifiers and edges
are labeled by "precedes"
and "strictly precedes" relationships among events induced by the constraints.
- Determine whether there is a cycle in G that contains a
"strictly precedes" edge. If so, then I is not valid.
-
If no
such cycle exists, and none of the impossibility constraints (section 5.3) and type constraints (section 5.4) are
violated, then I is valid.
A normal form of a PROV instance may not exist when a uniqueness constraint fails due to merging failure.
Two PROV instances are equivalent if they have the
isomorphic normal forms (that is, after applying all possible inference
rules, the two instances produce the same set of PROV statements,
up to reordering of statements and attributes within attribute lists,
and renaming of existential variables).
Equivalence has the following characteristics:
-
The order of provenance statements is irrelevant to the meaning of
a PROV instance. That is, a
PROV instance is equivalent to any other instance obtained by
permuting its statements.
- The order of attribute-value pairs in attribute lists is
irrelevant to the meaning of a PROV statement. That is, a PROV
statement carrying attributes is equivalent to any other statement
obtained by permuting attribute-value pairs.
- The particular choices of names of existential variables are irrelevant to the meaning
of an instance; that is, the names can be permuted without changing
the meaning. (Replacing two different names with equal names does
change the meaning.)
-
Applying inference rules, definitions, and uniqueness constraints preserves equivalence. That is, a PROV
instance is equivalent to the instance obtained by applying any
inference rule or definition, or by merging two statements to
enforce a uniqueness constraint.
- Equivalence is reflexive, symmetric, and transitive.
An application that processes PROV data should handle
equivalent instances in the same way. (Common exceptions to this rule
include, for example, pretty-printers that seek to preserve the
original order of statements in a file and avoid expanding
inferences.)
6.1 Bundles
The definitions, inferences, and constraints, and
the resulting notions of normalization, validity and equivalence,
assume a PROV instance with exactly one bundle, the toplevel
bundle, consisting of all PROV statements in the toplevel of the
instance (that is, not enclosed in a named bundle). In this section, we describe how to deal with PROV
instances consisting of multiple bundles. Briefly, each bundle is
handled independently; there is no interaction between bundles from
the perspective of applying definitions, inferences, or constraints,
computing normal forms, or checking validity or equivalence.
We model a general PROV instance, containing n named bundles
b1...bn, as a tuple
(B0,[b1=B1,...,bn=Bn])
where B0 is the set of
statements of the toplevel bundle, and for each i, Bi is the set of
statements of bundle bi. This notation is shorthand for the
following PROV-N syntax:
B0
bundle b1
B1
endBundle
...
bundle bn
Bn
endBundle
The normal form of a general PROV instance
(B0,[b1=B1,...,[bn=Bn]) is (B'0,[b1=B'1,...,bn=B'n])
where B'i is the normal
form of Bi for each i between 0 and n.
A general PROV instance is valid if each of the bundles B0,
..., Bn are valid and none of the bundle identifiers bi are repeated.
Two (valid) general PROV instances (B0,[b1=B1,...,bn=Bn]) and
(B'0,[b1'=B'1,...,b'm=B'm]) are equivalent if B0 is
equivalent to B'0 and n = m and
there exists a permutation P : {1..n} -> {1..n} such that for each i, bi =
b'P(i) and Bi is equivalent to B'P(i).