Rationale (Informative)
This section gives a high-level rationale that provides some further background for the constraints, but does not affect the technical content of the rest of the specification.
Entities, Activities and Agents
One of the central challenges in representing provenance information is how to deal with change. Real-world objects, information objects and Web resources change over time, and the characteristics that make them identifiable in a given situation are sometimes subject to change as well. PROV allows for things to be described in different ways, with different descriptions of their state.
An entity is a thing one wants to provide provenance for and whose situation in the world is described by some fixed attributes. An entity has a lifetime, defined as the period between its generation event and its invalidation event. An entity's attributes are established when the entity is created and (partially) describe the entity's situation and state during the entirety of the entity's lifetime.
A different entity (perhaps representing a different user or system perspective) may fix other aspects of the same thing, and its provenance may be different. Different entities that fix aspects of the same thing are called alternates, and the PROV relations of specializationOf and alternateOf can be used to link such entities.
Besides entities, a variety of other PROV objects and relationships carry attributes, including activity, generation, usage, invalidation, start, end, communication, attribution, association, delegation, and derivation. Each object has an associated duration interval (which may be a single time point), and attribute-value pairs for a given object are expected to be descriptions that hold for the object's duration.
However, the attributes of entities have special meaning because they are considered to be fixed aspects of underlying, changing things. This motivates constraints on alternateOf and specializationOf relating the attribute values of different entities.
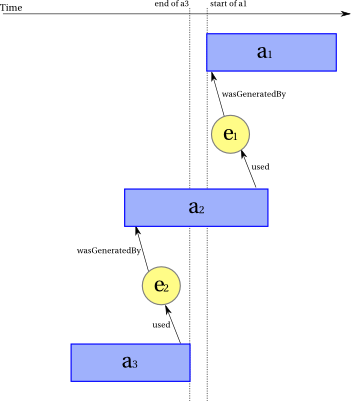
In order to describe the provenance of something during an interval over which relevant attributes of the thing are not fixed, a PROV instance would describe multiple entities, each with its own identifier, lifetime, and fixed attributes, and express dependencies between the various entities using events. For example, in order to describe the provenance of several versions of a document, involving attributes such as authorship that change over time, one can use different entities for the versions linked by appropriate generation, usage, revision, and invalidation events.
There is no assumption that the set of attributes listed in an entity statement is complete, nor that the attributes are independent or orthogonal of each other. Similarly, there is no assumption that the attributes of an entity uniquely identify it. Two different entities that present the same aspects of possibly different things can have the same attributes; this leads to potential ambiguity, which is mitigated through the use of identifiers.
An activity's lifetime is delimited by its start and its end events. It occurs over an interval delimited by two instantaneous events. However, an activity statement need not mention start or end time information, because they may not be known. An activity's attribute-value pairs are expected to describe the activity's situation during its lifetime.
An activity is not an entity. Indeed, an entity exists in full at any point in its lifetime, persists during this interval, and preserves the characteristics provided. In contrast, an activity is something that occurs, happens, unfolds, or develops through time. This distinction is similar to the distinction between 'continuant' and 'occurrent' in logic [[Logic]].
Events
Although time is important for provenance, provenance can be used in many different contexts within individual systems and across the Web. Different systems may use different clocks which may not be precisely synchronized, so when provenance statements are combined by different systems, an application may not be able to align the times involved to a single global timeline. Hence, PROV is designed to minimize assumptions about time. Instead, PROV talks about (identified) events.
The PROV data model is implicitly based on a notion of instantaneous events (or just events), that mark transitions in the world. Events include generation, usage, or invalidation of entities, as well as start or end of activities. This notion of event is not first-class in the data model, but it is useful for explaining its other concepts and its semantics [[PROV-SEM]]. Thus, events help justify inferences on provenance as well as validity constraints indicating when provenance is self-consistent.
Five kinds of instantaneous events are used in PROV. The activity start and activity end events delimit the beginning and the end of activities, respectively. The entity generation, entity usage, and entity invalidation events apply to entities, and the generation and invalidation events delimit the lifetime of an entity. More precisely:
An activity start event is the instantaneous event that marks the instant an activity starts.
An activity end event is the instantaneous event that marks the instant an activity ends.
An entity generation event is the instantaneous event that marks the final instant of an entity's creation timespan, after which it is available for use. The entity did not exist before this event.
An entity usage event is the instantaneous event that marks the first instant of an entity's consumption timespan by an activity. The described usage had not started before this instant, although the activity could potentially have used the same entity at a different time.
An entity invalidation event is the instantaneous event that marks the initial instant of the destruction, invalidation, or cessation of an entity, after which the entity is no longer available for use. The entity no longer exists after this event.
Types
As set out in other specifications, the identifiers used in PROV documents have associated type information. An identifier can have more than one type, reflecting subtyping or allowed overlap between types, and so we define a set of types of each identifier, typeOf(id). Some types are, however, required not to overlap (for example, no identifier can describe both an entity and an activity). In addition, an identifier cannot be used to identify both an object (that is, an entity, activity or agent) and a property (that is, a named event such as usage, generation, or a relationship such as attribution.) This specification includes disjointness and typing constraints that check these requirements. Here, we summarize the type constraints in Table 1.
| In relation... | identifier | has type(s)... |
|---|---|---|
| entity(e,attrs) | e | 'entity' |
| activity(a,t1,t2,attrs) | a | 'activity' |
| agent(ag,attrs) | ag | 'agent' |
| used(id; a,e,t,attrs) | e | 'entity' |
| a | 'activity' | |
| wasGeneratedBy(id; e,a,t,attrs) | e | 'entity' |
| a | 'activity' | |
| wasInformedBy(id; a2,a1,attrs) | a2 | 'activity' |
| a1 | 'activity' | |
| wasStartedBy(id; a2,e,a1,t,attrs) | a2 | 'activity' |
| e | 'entity' | |
| a1 | 'activity' | |
| wasEndedBy(id; a2,e,a1,t,attrs) | a2 | 'activity' |
| e | 'entity' | |
| a1 | 'activity' | |
| wasInvalidatedBy(id; e,a,t,attrs) | e | 'entity' |
| a | 'activity' | |
| wasDerivedFrom(id; e2,e1,a,g,u,attrs) | e2 | 'entity' |
| e1 | 'entity' | |
| a | 'activity' | |
| wasAttributedTo(id; e,ag,attr) | e | 'entity' |
| ag | 'agent' | |
| wasAssociatedWith(id; a,ag,pl,attrs) | a | 'activity' |
| ag | 'agent' | |
| pl | 'entity' | |
| actedOnBehalfOf(id; ag2,ag1,a,attrs) | ag2 | 'agent' |
| ag1 | 'agent' | |
| a | 'activity' | |
| alternateOf(e1,e2) | e1 | 'entity' |
| e2 | 'entity' | |
| specializationOf(e1,e2) | e1 | 'entity' |
| e2 | 'entity' | |
| hadMember(c,e) | c | 'entity' 'prov:Collection' |
| e | 'entity' | |
| entity(c,[prov:type='prov:EmptyCollection,...]) | c | 'entity' 'prov:Collection' 'prov:EmptyCollection' |
Validation Process Overview
This section collects common concepts and operations that are used throughout the specification, and relates them to background terminology and ideas from logic [[Logic]], constraint programming [[CHR]], and database constraints [[DBCONSTRAINTS]]. This section does not attempt to provide a complete introduction to these topics, but it is provided in order to aid readers familiar with one or more of these topics in understanding the specification, and to clarify some of the motivations for choices in the specification to all readers.
As discussed below, the definitions, inferences and constraints can be viewed as pure logical assertions that could be checked in a variety of ways. The rest of this document specifies validity and equivalence procedurally, that is, in terms of a reference implementation based on normalization. Although both declarative and procedural specification techniques have advantages, a purely declarative specification offers much less guidance for implementers, while the procedural approach adopted here immediately demonstrates implementability and provides an adequate (polynomial-time) default implementation. In this section we relate the declarative meaning of formulas to their procedural meaning. [[PROV-SEM]] provides an alternative, declarative characterization of validity which could be used as a starting point for other implementation strategies.
Constants, Variables and Placeholders
PROV statements involve identifiers, literals, placeholders, and attribute lists. Identifiers are, according to PROV-N, expressed as qualified names which can be mapped to URIs [[!RFC3987]]. However, in order to specify constraints over PROV instances, we also need variables that represent unknown identifiers, literals, or placeholders. These variables are similar to those in first-order logic [[Logic]]. A variable is a symbol that can be replaced by other symbols, including either other variables or constant identifiers, literals, or placeholders. In a few special cases, we also use variables for unknown attribute lists. To help distinguish identifiers and variables, we also term the former 'constant identifiers' to highlight their non-variable nature.
Several definitions and inferences conclude by saying that some objects exist such that some other formulas hold. Such an inference introduces fresh existential variables into the instance. An existential variable denotes a fixed object that exists, but its exact identity is unknown. Existential variables can stand for unknown identifiers or literal values only; we do not allow existential variables that stand for unknown attribute lists.
In particular, many occurrences of the placeholder symbol - stand for unknown objects; these are handled by expanding them to existential variables. Some placeholders, however, indicate the absence of an object, rather than an unknown object. In other words, the placeholder is overloaded, with different meanings in different places.
An expression is called a term if it is either a constant identifier, literal, placeholder, or variable. We write t to denote an arbitrary term.
Substitution
A substitution is a function that maps variables to terms. Concretely, since we only need to consider substitutions of finite sets of variables, we can write substitutions as [x1 = t1,...,xn=tn]. A substitution S = [x1 = t1,...,xn=tn] can be applied to a term by replacing occurrences of x_i with t_i.
In addition, a substitution can be applied to an atomic formula (PROV statement) p(t1,...,tn) by applying it to each term, that is, S(p(t1,...,tn)) = p(S(t1),...,S(tn)). Likewise, a substitution S can be applied to an instance I by applying it to each atomic formula (PROV statement) in I, that is, S(I) = {S(A) | A ∈ I}.
Formulas
For the purpose of constraint checking, we view PROV statements (possibly involving existential variables) as formulas. An instance is analogous to a "theory" in logic, that is, a set of formulas all thought to describe the same situation. The set can also be thought of a single, large formula: the conjunction of all of the atomic formulas.
The atomic constraints considered in this specification can be viewed as atomic formulas:
- Uniqueness constraints employ atomic equational formulas t = t'.
- Ordering constraints employ atomic precedence relations that can be thought of as binary formulas precedes(t,t') or strictlyPrecedes(t,t')
- Typing constraints 'type' ∈ typeOf(id) can be represented as a atomic formulas typeOf(id,'type').
- Impossibility constraints employ the conclusion INVALID, which is equivalent to the logical constant False.
Similarly, the definitions, inferences, and constraint rules in this specification can also be viewed as logical formulas, built up out of atomic formulas, logical connectives "and" (∧), "implies" (⇒), and quantifiers "for all" (∀) and "there exists" (∃). For more background on logical formulas, see a logic textbook such as [[Logic]].
- A definition of the form "A IF AND ONLY IF there exists y1...ym such that B1 and ... and Bk" can be thought of as a formula ∀ x1,....,xn. A ⇔ ∃ y1...ym . B1 ∧ ... ∧ Bk, where x1...xn are the free variables of the definition.
- An inference of the form "IF A1 and ... and Ap THEN there exists y1...ym such that B1 and ... and Bk" can be thought of as a formula ∀ x1,....,xn. A1 ∧ ... ∧ Ap ⇒ ∃ y1...ym . B1 ∧ ... ∧ Bk, where x1...xn are the free variables of the inference.
- A uniqueness, ordering, or typing constraint of the form "IF A1 ∧ ... ∧ Ap THEN C" can be viewed as a formula ∀ x1...xn. A1 ∧ ... ∧ Ap ⇒ C.
- A constraint of the form "IF A1 ∧ ... ∧ Ap THEN INVALID" can be viewed as a formula ∀ x1...xn. A1 ∧ ... ∧ Ap ⇒ False.
Satisfying definitions, inferences, and constraints
In logic, a formula's meaning is defined by saying when it is satisfied. We can view definitions, inferences, and constraints as being satisfied or not satisfied in a PROV instance, augmented with information about the constraints.
- A logical equivalence as used in a definition is satisfied when the formula ∀ x1,....,xn. A ⇔ ∃ y1...ym . B1 ∧ ... ∧ Bk holds, that is, for any substitution of the variables x1,....,xn, formula A and formula ∃ y1...ym. B1 ∧ ... ∧ Bk are either both true or both false.
- A logical implication as used in an inference is satisfied when the formula ∀ x1,....,xn. A1 ∧ ... ∧ Ap ⇒ ∃ y1...ym . B1 ∧ ... ∧ Bk holds, that is, for any substitution of the variables x1,....,xn, if A1 ∧ ... ∧ Ap is true, then for some further substitution of terms for variables y1...ym, formula B1 ∧ ... ∧ Bk is also true.
- A uniqueness, ordering, or typing constraint is satisfied when its associated formula ∀ x1...xn. A1 ∧ ... ∧ Ap ⇒ C holds, that is, for any substitution of the variables x1,....,xn, if A1 ∧ ... ∧ Ap is true, then C is also true.
- An impossibility constraint is satisfied when the formula ∀ x1...xn. A1 ∧ ... ∧ Ap ⇒ False holds. This is logically equivalent to ∄ x1...xn. A1 ∧ ... ∧ Ap, that is, there exists no substitution for x1...xn making A1 ∧ ... ∧ Ap true.
Unification and Merging
Unification is an operation that takes two terms and compares them to determine whether they can be made equal by substituting an existential variable with another term. If so, the result is such a substitution; otherwise, the result is failure. Unification is an essential concept in logic programming and automated reasoning, where terms can involve variables, constants and function symbols. In PROV, by comparison, unification only needs to deal with variables, constants and literals.
Unifying two terms t,t' results in either substitution S such that S(t) = S(t'), or failure indicating that there is no substitution that can be applied to both t and t' to make them equal. Unification is also used to define an operation on PROV statements called merging. Merging takes two statements that have equal identifiers, unifies their corresponding term arguments, and combines their attribute lists.
Applying definitions, inferences, and constraints
Formulas can also be interpreted as having computational content. That is, if an instance does not satisfy a formula, we can often apply the formula to the instance to produce another instance that does satisfy the formula. Definitions, inferences, and uniqueness constraints can be applied to instances:
- A definition of the form ∀ x1,....,xn. A ⇔ ∃ y1...ym . B1 ∧ ... ∧ Bk can be applied by searching for any occurrences of A in the instance and adding B1, ..., Bk, generating fresh existential variables y1,...,ym, and conversely, whenever there is an occurrence of B1, ..., Bk, adding A. In our setting, the defined formulas A are never used in other formulas, so it is sufficient to replace all occurrences of A with their definitions. The formula A is then redundant, and can be removed from the instance.
- An inference of the form ∀ x1,....,xn. A1 ∧ ... ∧ Ap ⇒ ∃ y1...ym . B1 ∧ ... ∧ Bk can be applied by searching for any occurrences of A1 ∧ ... ∧ Ap in the instance and, for each such match for which the entire conclusion does not already hold (for some y1,...,ym), adding B1 ∧ ... ∧ Bk to the instance, generating fresh existential variables y1,...,ym.
- A uniqueness constraint of the form ∀ x1...xn. A1 ∧ ... ∧ Ap ⇒ t = t' can be applied by searching for an occurrence A1 ∧ ... ∧ Ap in the instance, and if one is found, unifying the terms t and t'. If successful, the resulting substitution is applied to the instance; otherwise, the application of the uniqueness constraint fails.
- A key constraint can similarly be applied by searching for different occurrences of a statement with the same identifier, unifying the corresponding parameters of the statements, and concatenating their attribute lists, to form a single statement. The substitutions obtained by unification are applied to the merged statement and the rest of the instance.
As noted above, uniqueness or key constraint application can fail, if a required unification or merging step fails. Failure of constraint application means that there is no way to add information to the instance to satisfy the constraint, which in turn implies that the instance is invalid.
The process of applying definitions, inferences, and constraints to a PROV instance until all of them are satisfied is similar to what is sometimes called chasing [[DBCONSTRAINTS]] or saturation [[CHR]]. We call this process normalization.
Although this specification outlines one particular way of performing inferences and checking constraints, based on normalization, implementations can use any other equivalent algorithm. The logical formulas corresponding to the definitions, inferences, and constraints outlined above (and further elaborated in [[PROV-SEM]]) provides an equivalent specification, and any implementation that correctly checks validity and equivalence (whether it performs normalization or not) complies with this specification.
Termination
In general, applying sets of logical formulas of the above definition, inference, and constraint forms is not guaranteed to terminate. A simple example is the inference R(x,y) ⇒ ∃z. R(x,z) ∧R(z,y), which can be applied to {R(a,b)} to generate an infinite sequence of larger and larger instances. To ensure that normalization, validity, and equivalence are decidable, we require that normalization terminates. There is a great deal of work on termination of the chase in databases, or of sets of constraint handling rules. The termination of the notion of normalization defined in this specification is guaranteed because the definitions, inferences and uniqueness/key constraints correspond to a weakly acyclic set of tuple-generating and equality-generating dependencies, in the terminology of [[DBCONSTRAINTS]]. The termination of the remaining ordering, typing, and impossibility constraints is easy to show. Appendix A gives a proof that the definitions, inferences, and uniqueness and key constraints are weakly acyclic and therefore terminating.
There is an important subtlety that is essential to guarantee termination. This specification draws a distinction between knowing that an identifier has type 'entity', 'activity', or 'agent', and having an explicit entity(id), activity(id), or agent(id) statement in the instance. For example, focusing on entity statements, we can infer 'entity' ∈ typeOf(id) if entity(id) holds in the instance. In contrast, if we only know that 'entity' ∈ typeOf(id), this does not imply that entity(id) holds.
This distinction (for both entities and activities) is essential to ensure termination of the inferences, because we allow inferring that a declared entity(id,attrs) has a generation and invalidation event, using TBD. Likewise, for activities, we allow inferring that a declared activity(id,t1,t2,attrs) has a generation and invalidation event, using TBD. These inferences do not apply to identifiers whose types are known, but for which there is not an explicit entity or activity statement. If we strengthened the type inference constraints to add new entity or activity statements for the entities and activities involved in generating or starting other declared entities or activities, then we could keep generating new entities and activities in an unbounded chain into the past (as in the "chicken and egg" paradox). The design adopted here requires that instances explicitly declare the entities and activities that are relevant for validity checking, and only these can be inferred to have invalidation/generation and start/end events. This inference is not supported for identifiers that are indirectly referenced in other relations and therefore have type 'entity' or 'activity'.
Checking ordering, typing, and impossibility constraints
The ordering, typing, and impossibility constraints are checked rather than applied. This means that they do not generate new formulas expressible in PROV, but they do generate basic constraints that might or might not be consistent with each other. Checking such constraints follows a saturation strategy similar to that for normalization:
For ordering constraints, we check by generating all of the precedes and strictly-precedes relationships specified by the rules. These can be thought of as a directed graph whose nodes are terms, and whose edges are precedes or strictly-precedes relationships. An ordering constraint of the form ∀ x1...xn. A1 ∧ ... ∧ Ap ⇒ precedes(t,t') can be applied by searching for occurrences of A1 ∧ ... ∧ Ap and for each such match adding the atomic formula precedes(t,t') to the instance, and similarly for strictly-precedes constraints. After all such constraints have been checked, and the resulting edges added to the graph, the ordering constraints are violated if there is a cycle in the graph that includes a strictly-precedes edge, and satisfied otherwise.
For typing constraints, we check by constructing a function typeOf(id) mapping identifiers to sets of possible types. We start with a function mapping each identifier to the empty set, reflecting no constraints on the identifiers' types. A typing constraint of the form ∀ x1...xn. A1 ∧ ... ∧ Ap ⇒ 'type' ∈ typeOf(id) is checked by adjusting the function by adding 'type' to typeOf(id) for each conclusion 'type' ∈ typeOf(id) of the rule. Typing constraints with multiple conclusions are handled analogously. Once all constraints have been checked in all possible ways, we check that the disjointness constraints hold of the resulting typeOf function. (These are essentially impossibility constraints).
For impossibility constraints, we check by searching for the forbidden pattern that the impossibility constraint describes. Any match of this pattern leads to failure of the constraint checking process. An impossibility constraint of the form ∀ x1...xn. A1 ∧ ... ∧ Ap ⇒ False can be applied by searching for occurrences of A1 ∧ ... ∧ Ap in the instance, and if any such occurrence is found, signaling failure.
A normalized instance that passes all of the ordering, typing, and impossibility constraint checks is called valid. Validity can be, but is not required to be, checked by normalizing and then checking constraints. Any other algorithm that provides equivalent behavior (that is, accepts the same valid instances and rejects the same invalid instances) is allowed. In particular, the checked constraints and the applied definitions, inferences and uniqueness constraints do not interfere with one another, so it is also possible to mix checking and application. This may be desirable in order to detect invalidity more quickly.
Equivalence and Isomorphism
Given two normal forms, a natural question is whether they contain the same information, that is, whether they are equivalent (if so, then the original instances are also equivalent.) By analogy with logic, if we consider normalized PROV instances with existential variables to represent sets of possible situations, then two normal forms may describe the same situation but differ in inessential details such as the order of statements or of elements of attribute-value lists. To remedy this, we can easily consider instances to be equivalent up to reordering of attributes. However, instances can also be equivalent if they differ only in choice of names of existential variables. Because of this, the appropriate notion of equivalence of normal forms is isomorphism. Two instances I1 and I2 are isomorphic if there is an invertible substitution S mapping existential variables to existential variables such that S(I1) = I2.
Equivalence can be checked by normalizing instances, checking that both instances are valid, then testing whether the two normal forms are isomorphic. (It is technically possible for two invalid normal forms to be isomorphic, but to be considered equivalent, the two instances must also be valid.) As with validity, the algorithm suggested by this specification is just one of many possible ways to implement equivalence checking; it is not required that implementations compute normal forms explicitly, only that their determinations of equivalence match those obtained by the algorithm in this specification.
Equivalence is only explicitly specified for valid instances (whose normal forms exist and are unique up to isomorphism). Implementations may test equivalences involving valid and invalid documents. This specification does not constrain the behavior of equivalence checking involving invalid instances, provided that:
- instance equivalence is reflexive, symmetric and transitive on all instances
- no valid instance is equivalent to an invalid instance.
Because of the second constraint, equivalence is essentially the union of two equivalence relations on the disjoint sets of valid and invalid instances. There are two simple implementations of equivalence for invalid documents that are correct:
- each invalid instance is equivalent only to itself
- every pair of invalid instances are equivalent
From Instances to Bundles and Documents
PROV documents can contain multiple instances: a toplevel instance, and zero or more additional, named instances called bundles. For the purpose of inference and constraint checking, these instances are treated independently. That is, a PROV document is valid provided that each instance in it is valid and the names of its bundles are distinct. In other words, there are no validity constraints that need to be checked across the different instances in a PROV document; the contents of one instance in a multi-instance PROV document cannot affect the validity of another instance. Similarly, a PROV document is equivalent to another if their toplevel instances are equivalent, they have the same number of bundles with the same names, and the instances of their corresponding bundles are equivalent. The scope of an existential variable in PROV is delimited at the instance level. This means that occurrences of existential variables with the same name appearing in different statements within the same instance stand for a common, unknown term. However, existential variables with the same name occurring in different instances do not necessarily denote the same term. This is a consequence of the fact that the instances of two equivalent documents only need to be pairwise isomorphic; this is a weaker property than requiring that there be a single isomorphism that works for all of the corresponding instances.
Summary of inferences and constraints
Table 2 summarizes the inferences, and constraints specified in this document, broken down by component and type or relation involved.
| Type or Relation Name | Inferences and Constraints | Component |
| Entity | TBD TBD TBD TBD TBD |
1 |
| Activity | TBD TBD TBD TBD TBD TBD |
|
| Generation | TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD |
|
| Usage | TBD TBD TBD TBD TBD TBD TBD TBD TBD |
|
| Communication | TBD TBD TBD TBD TBD TBD |
|
| Start | TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD |
|
| End | TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD |
|
| Invalidation | TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD TBD |
|
| Derivation | TBD TBD TBD TBD TBD TBD |
2 |
| Revision | TBD |
|
| Quotation | No specific constraints | |
| Primary Source | No specific constraints | |
| Influence | No specific constraints | |
| Agent | TBD TBD |
3 |
| Attribution | TBD TBD TBD TBD TBD TBD |
|
| Association | TBD TBD TBD TBD TBD |
|
| Delegation | TBD TBD TBD TBD TBD TBD |
|
| Influence | TBD TBD |
|
| Bundle constructor | No specific constraints; see | 4 |
| Bundle type | No specific constraints; see | |
| Alternate | TBD TBD TBD TBD |
5 |
| Specialization | TBD TBD TBD TBD TBD TBD TBD |
|
| Collection | No specific constraints | 6 |
| Membership | TBD TBD |