PROV-DM Types and Relations
Provenance concepts, expressed as PROV-DM types and relations, are organized according to six components that are defined in this section. The components and their dependencies are illustrated in Figure 4. A component that relies on concepts defined in another is displayed above it in the figure. So, for example, component 6 (collections) depends on concepts defined in component 3 (derivation), itself dependen on concepts defined in component 1 (entity and activity).
- Component 1: entities and activities. The first component consists of entities, activities, and concepts linking them, such as generation, usage, start, end. The first component is the only one comprising time-related concepts.
- Component 2: derivations. The second component is formed with derivations and derivation subtypes.
- Component 3: agents and responsibility. The third component consists of agents and concepts ascribing responsibility to agents.
- Component 4: bundles. The fourth component is concerned with bundles, a mechanism to support provenance of provenance.
- Component 5: alternate. The fifth component consists of relations linking entities referring to the same thing.
- Component 6: collections. The sixth component is about collections and concepts capturing their transformation, such as insertion and removal.
Component 6: Collections
The sixth component of PROV-DM is concerned with the notion of collections. A collection is an entity that has some members. The members are themselves entities, and therefore their provenance can be expressed. Some applications need to be able to express the provenance of the collection itself: e.g. who maintains the collection (attribution), which members it contains as it evolves, and how it was assembled. The purpose of Component 6 is to define the types and relations that are useful to express the provenance of collections. In PROV, the concept of Collection is implemented by means of dictionaries, which we introduce in this section.
Figure 10 depicts the sixth component with four new classes (Collection, Dictionary, EmptyDictionary, and Pair) and three associations (insertion, removal, and memberOf).
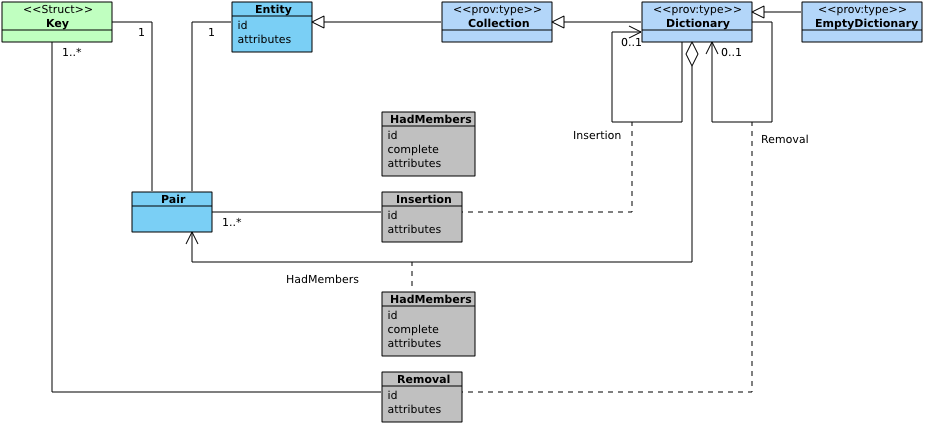
The intent of these relations and types is to express the history of changes that occurred to a collection. Changes to collections are about the insertion of entities into, and the removal of entities from the collection. Indirectly, such history provides a way to reconstruct the contents of the collection.
Collection
A collection is a multiset of entities (it is a multiset, rather than a set, because it may not be possible to verify that two distinct entity identitifiers do not denote, in fact, the same entity).
PROV-DM defines the following types related to collections:
- prov:Collection denotes an entity of type Collection, i.e. an entity that can participate in relations amongst collections;
- prov:EmptyCollection denotes an empty collection.
entity(c0, [prov:type='prov:EmptyCollection' ]) // c0 is an empty collection entity(c1, [prov:type='prov:Collection' ]) // c1 is a collection, with unknown content
In PROV, the concept of Collection is provided as an extensibility point for specialized kinds of collections. One of these, Dictionary, is defined next.
Collection Memberhsip
A collection membership relation is defined, to allow stating the members of a Collection.
- id: an OPTIONAL identifier identifying the relation;
- collection: an identifier (c) for the collection whose members are asserted;
- entity-set: a set of entities e_1, ..., e_n that are members of the collection;
- complete: an OPTIONAL boolean
Value (cplt). It is interpreted as follows:
- if it is present and set to true, then c is believed to include all and only the members specified in the entity-set;
- if it is present and set to false, then c is believed to include more members in addition to those specified in the entity-set;
- if it is not present, then c is believed to include all the members specified in the entity-set, and it MAY include more.
- attributes: an OPTIONAL set (attrs) of attribute-value pairs representing additional information about this relation.
Note that the attribute complete indicates that the membership relation provides a complete description of the collection membership. It is possible for different provenance descriptions to provide different membership statements regarding the same collection. The resolution of any potential conflict amongst such membership statements is defined by applications.
Dictionary
PROV-DM defines a specific type of collection, specified as follows.
Conceptually, a dictionary has a logical structure consisting of key-entity pairs. This structure is often referred to as a map, and is a generic indexing mechanism that can abstract commonly used data structures, including associative lists, relational tables, ordered lists, and more. The specification of such specialized structures in terms of key-value pairs is out of the scope of this document.
A given dictionary forms a given structure for its members. A different structure (obtained either by insertion or removal of members) constitutes a different dictionary. Hence, for the purpose of provenance, a dictionary entity is viewed as a snapshot of a structure. Insertion and removal operations result in new snapshots, each snapshot forming an identifiable dictionary entity.
Following the earlier definitions for generic collections, PROV-DM defines the following types related to dictionaries:
- prov:Dictionary is a subtype of prov:Collection. It denotes an entity of type dictionary, i.e. an entity that can participate in relations amongst dictionaries;
- prov:EmptyDictionary is a subtype of prov:EmptyCollection. It denotes an empty dictionary.
entity(d0, [prov:type='prov:EmptyDictionary' ]) // d0 is an empty dictionary entity(d1, [prov:type='prov:Dictionary' ]) // d1 is a dictionary, with unknown content
Dictionary Membership
The dictionary membership has the same purpose as the collection membership relation, but it applies to entities having prov:type = 'prov:Dictionary'. It allows stating the members of a Dictionary.
- id: an OPTIONAL identifier identifying the relation;
- dictionary: an identifier (c) for the dictionary whose members are asserted;
- key-entity-set: a set of key-entity pairs (key_1, e_1), ..., (key_n, e_n) that are members of the dictionary;
- complete: an OPTIONAL boolean
Value (cplt). It is interpreted as follows:
- if it is present and set to true, then c is believed to include all and only the members specified in the key-entity-set;
- if it is present and set to false, then c is believed to include more members in addition to those specified in the key-entity-set;
- if it is not present, then c is believed to include all the members specified in the key-entity-set, and it MAY include more.
- attributes: an OPTIONAL set (attrs) of attribute-value pairs representing additional information about this relation.
The attribute complete is interpreted as for the general collection membership relation.
entity(d1, [prov:type='prov:Dictionary' ]) // d1 is a dictionary, with unknown content
entity(d2, [prov:type='prov:Dictionary' ]) // d2 is a dictionary, with unknown content
entity(e1)
entity(e2)
memberOf(d1, {("k1", e1), ("k2", e2)} )
memberOf(d2, {("k1", e1), ("k2", e2)}, true)
From these descriptions, we conclude:
- d1 has the following pairs as members: ("k1", e1), ("k2", e2), and may contain others.
- d2 exactly has the following pairs as members: ("k1", e1), ("k2", e2), and does not contain any other.
Thus, the membership of d1 is only partially known.
Dictionary Insertion
An Insertion relation, written derivedByInsertionFrom(id; d2, d1, {(key_1, e_1), ..., (key_n, e_n)}, attrs), has:
- id: an OPTIONAL identifier identifying the relation;
- after: an identifier (d2) for the dictionary after insertion;
- before: an identifier (d1) for the dictionary before insertion;
- key-entity-set: the inserted key-entity pairs (key_1, e_1), ..., (key_n, e_n) in which each key_i is a value, and e_i is an identifier for the entity that has been inserted with the key; each key_i is expected to be unique for the key-entity-set;
- attributes: an OPTIONAL set (attrs) of attribute-value pairs representing additional information about this relation.
An Insertion relation derivedByInsertionFrom(id; d2, d1, {(key_1, e_1), ..., (key_n, e_n)}) states that d2 is the dictionary following the insertion of pairs (key_1, e_1), ..., (key_n, e_n) into dictionary d1.
entity(d0, [prov:type='prov:EmptyDictionary' ]) // d0 is an empty dictionary
entity(e1)
entity(e2)
entity(e3)
entity(d1, [prov:type='prov:Dictionary' ])
entity(d2, [prov:type='prov:Dictionary' ])
derivedByInsertionFrom(d1, d0, {("k1", e1), ("k2", e2)})
derivedByInsertionFrom(d2, d1, {("k3", e3)})
From this set of descriptions, we conclude:
- d0 is the set { }
- d1 is the set { ("k1", e1), ("k2", e2) }
- d2 is the set { ("k1", e1), ("k2", e2), ("k3", e3) }
Insertion provides an "update semantics" for the keys that are already present in a dictionary, since a new pair replaces an existing pair with the same key in the new dictionary. This is illustrated by the following example.
entity(d0, [prov:type='prov:EmptyDictionary' ]) // d0 is an empty dictionary
entity(e1)
entity(e2)
entity(e3)
entity(d1, [prov:type='prov:Dictionary' ])
entity(d2, [prov:type='prov:Dictionary' ])
derivedByInsertionFrom(d1, d0, {("k1", e1), ("k2", e2)})
derivedByInsertionFrom(d2, d1, {("k1", e3)})
This is a case of update of e1 to e3 for the same key, "k1". From this set of descriptions, we conclude:
- d0 is the set { }
- d1 is the set { ("k1", e1), ("k2", e2) }
- d2 is the set { ("k1", e3), ("k2", e2) }
Dictionary Removal
A Removal relation, written derivedByRemovalFrom(id; d2, d1, {key_1, ... key_n}, attrs), has:
- id: an OPTIONAL identifier identifying the relation;
- after: an identifier (d2) for the dictionary after the deletion;
- before: an identifier (d1) for the dictionary before the deletion;
- key-set: a set of deleted keys key_1, ..., key_n, for which each key_i is a value;
- attributes: an OPTIONAL set (attrs) of attribute-value pairs representing additional information about this relation.
A Removal relation derivedByRemovalFrom(id; d2,d1, {key_1, ..., key_n}) states that d2 is the dictionary following the removal of the set of pairs corresponding to keys key_1...key_n from d1.
entity(d0, [prov:type="prov:EmptyDictionary"]) // d0 is an empty dictionary
entity(e1)
entity(e2)
entity(e3)
entity(d1, [prov:type="prov:Dictionary"])
entity(d2, [prov:type="prov:Dictionary"])
derivedByInsertionFrom(d1, d0, {("k1", e1), ("k2",e2)})
derivedByInsertionFrom(d2, d1, {("k3", e3)})
derivedByRemovalFrom(d3, d2, {"k1", "k3"})
From this set of descriptions, we conclude:
- d0 is the set { }
- d1 is the set { ("k1", e1), ("k2", e2) }
- d2 is the set { ("k1", e1), ("k2", e2), ("k3", e3) }
- d3 is the set { ("k2", e2) }
Further considerations:
- The representation of a dictionary through these relations makes no assumption regarding the underlying data structure used to store and manage dictionaries. In particular, no assumptions are needed regarding the mutability of a data structure that is subject to updates. Entities, however, are immutable and this applies to those entities that represent dictionaries. This is reflected in the constraints listed in [[PROV-CONSTRAINTS]].